How RF Filters work on separating signals?
The working principle of RF filter
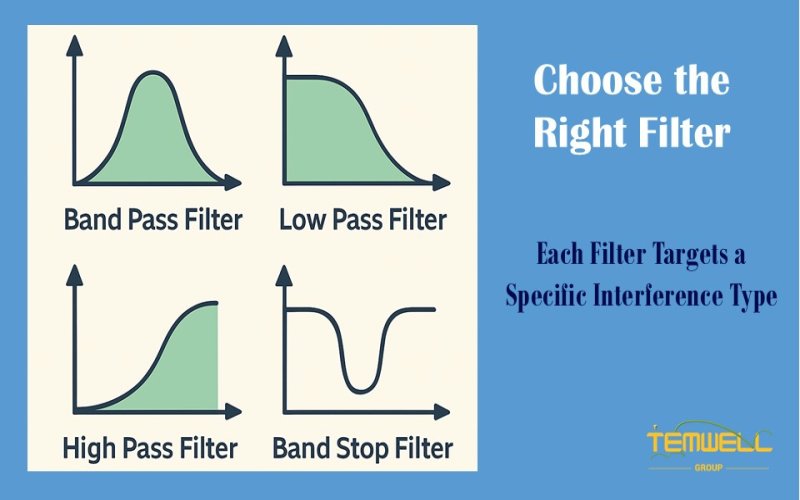
The core function of RF filter is to allow signals within a specific frequency band to pass through (Passband) while suppressing or blocking signals in other unwanted frequency bands (Stopband). Common types of filters include low-pass, high-pass, band-pass, and band-stop filters.
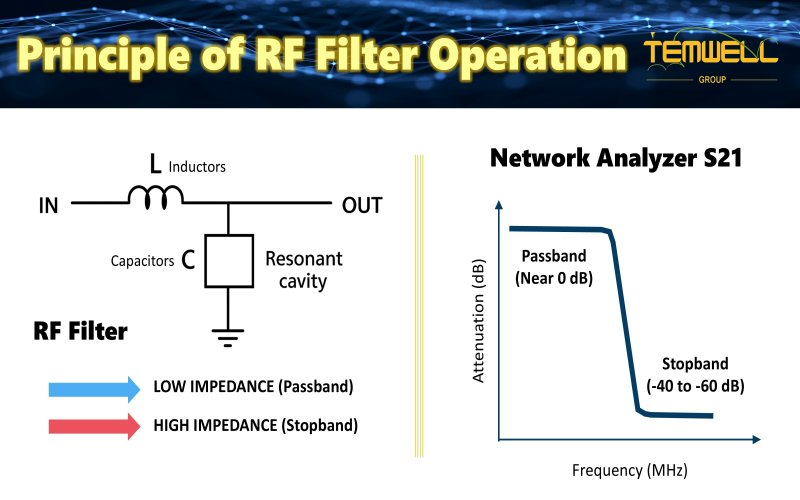
RF Filters selectively allow or block signals, their core principle stemming from the different characteristics of inductors, capacitors, or resonant cavities at different frequencies. These components exhibit "selective impedance" to signals at different frequencies. That is, they present low impedance at some frequencies, allowing energy to pass through, while presenting high impedance at other frequencies, causing the signal to be reflected or weakened. When the components in a circuit are combined to form specific resonant conditions, a "pass region" and a "blocking region" are naturally established. The pass region allows energy of specific frequencies to be transferred efficiently, while the blocking region significantly attenuates energy of unwanted frequencies. Filtering behavior is essentially a "frequency selection" effect, utilizing the physical response of the components themselves to enable the circuit to automatically divide the signal into usable and unusable parts, achieving signal purification and interference suppression.
Take a bandpass filter as an example. Its design causes the circuit to resonate in a specific frequency range. At this point, the impedance decreases, allowing signal energy to pass smoothly, forming a "pass band." When the signal frequency leaves this resonant region, the circuit impedance rises rapidly, causing signals at these frequencies to be reflected back to the source or absorbed within the circuit, forming a "blocking band." On the S21 curve of a network analyzer, the pass band will show a high transmission range close to 0 dB, while the S21 value of the blocking band will drop to low values such as -40 dB or -60 dB, indicating that the filter successfully suppresses unwanted signals.
Therefore, it can be seen that RF filters do not weaken all signals, but rather utilize the resonant characteristics of the structure to accurately determine which frequencies should be passed and which should be suppressed, so that the system can maintain a pure and stable signal quality.
How 4 main kinds of RF filters isolate signals
The operating principle of RF filter stems from the different responses of inductors and capacitors to different frequencies. Through various arrangements and combinations of these components, various types of filters can be formed, achieving the characteristic of selectively passing or blocking specific frequencies.
1. Bandpass Filter (BPF) – Passes only a specified frequency band.
The core principle of a bandpass filter comes from the resonance phenomenon formed by the inductor (L) and capacitor (C). LC exhibits the lowest impedance at a specific frequency f₀, allowing signal energy to pass through almost unimpeded; however, when the signal frequency deviates from f₀, the impedance of L and C increases rapidly, causing the signal to be reflected or diverted to other paths and absorbed. This "frequency-selective impedance" is the essence of filtering. On a network analyzer, the S21 curve approaches 0 dB in the passband and drops to -40 dB and -60 dB in the stopband, indicating that unwanted frequencies are effectively suppressed. Bandpass filters are widely used in wireless communications, radar, and RF modules to ensure that the system obtains a clean target signal.
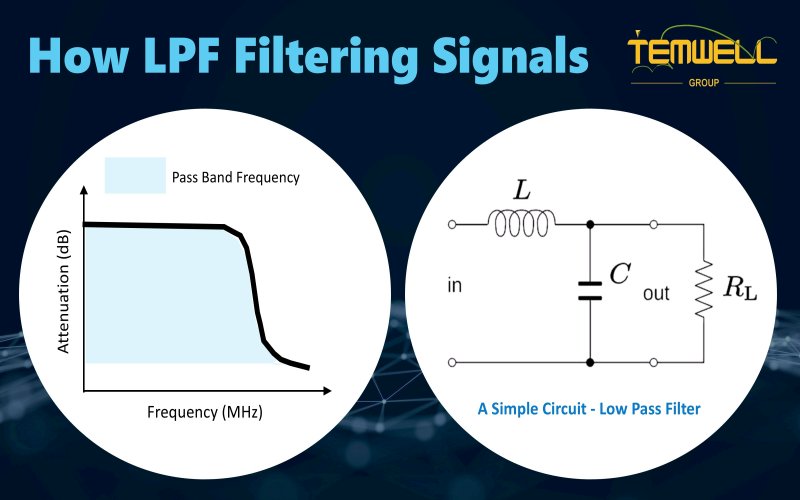
2. Low-Pass Filter (LPF) – Passes low frequencies and blocks high frequencies
Low-pass filters selectively filter signals by utilizing the differences in the responses of inductors and capacitors to different frequencies. An inductor (L) exhibits high impedance at high frequencies, blocking rapidly changing signals; a capacitor (C) has lower impedance at high frequencies, directing high-frequency energy to ground. When the two work together, low frequencies can pass through smoothly, while high-frequency signals are suppressed or absorbed. This structure naturally creates a "cutoff frequency," clearly demarcating the passband and stopband. In the S21 test curve, the low-frequency region remains near 0 dB, while the curve drops rapidly above the cutoff frequency. Low-pass filters (LPFs) are commonly used to suppress noise, filter high-frequency interference, and eliminate harmonics, making them fundamental filtering components in various power supply, communication, and signal processing systems.
3. High-pass filter (HPF) – blocks low frequencies and passes high frequencies.
The principle of a high-pass filter is to utilize the inverse combination of the properties of capacitors blocking low frequencies and inductors blocking high frequencies. Capacitors have extremely high impedance at low frequencies, blocking slowly changing signals (such as low-frequency noise or DC); as the frequency increases, the impedance decreases, allowing high-frequency signals to pass through smoothly. Simultaneously, inductors exhibit low impedance at low frequencies, effectively guiding low-frequency noise away from the main path and absorbing it. This combination allows the filter to exhibit good transmission at high frequencies and strong attenuation at low frequencies. In the S21 curve, it can be observed that the low-frequency region drops to -20 dB and -40 dB, while the high-frequency region is close to 0 dB. High-pass filters are commonly used in communication receivers, audio systems, and electronic devices that require the removal of low-frequency interference.
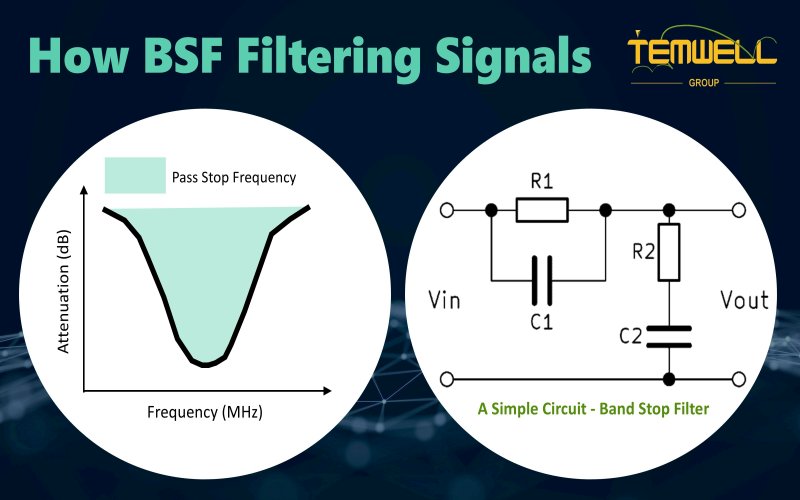
4 Band-stop filter (BSF / Notch Filter） – blocks specific frequencies.
Unlike bandpass filters, bandstop filters utilize the anti-resonance created by the LC circuit to block specific frequencies. When the signal frequency falls at the anti-resonance point of the LC circuit, the circuit exhibits extremely high impedance, completely preventing energy from passing through at that frequency. The S21 curve will show a deep trough at this frequency (e.g., -50 dB to -80 dB). In other frequency ranges, the circuit maintains low impedance, allowing the signal to transmit smoothly. Bandstop filters are particularly suitable for removing single sources of interference, such as noise frequencies in wireless equipment, Wi-Fi interference, or fixed-frequency noise from industrial machinery. Their high selectivity and strong suppression capabilities make them crucial in EMI, RF receiving systems, and medical equipment.
Determining the performance of RF filters (BPF/ LPF/ HPF/ BSF)
After understanding the operating principles and internal structure of filters, the next step is to learn how to evaluate the performance of various filters. Different filters have different evaluation criteria, and familiarity with these methods is essential for selecting the right filter and achieving its best performance.
1. Performance Evaluation of Bandpass Filters (BPF)
The key to evaluating the performance of a bandpass filter lies in its passband quality and stopband rejection. First, the insertion loss (IL) in the passband should be as low as possible; generally, less than 1 dB represents excellent performance, and less than 0.5 dB indicates a high-performance product. Simultaneously, better passband flatness indicates a more uniform frequency response and less impact on system gain. Second, the stopband rejection must be checked. Ideally, it should reach -40 dB, -60 dB, or even higher after a certain frequency difference from the passband to effectively isolate interference signals. Center frequency stability is also an indicator of quality. If the filter drifts due to temperature, power, or structural changes, it will cause system frequency misalignment. In summary, the overall quality of a BPF can be judged from IL, rejection, flatness, and stability.
2. Performance Evaluation of Low-Pass Filters (LPF)
The performance of a low-pass filter should be evaluated from three aspects: passband loss, cutoff characteristics, and high-frequency suppression. The insertion loss within the passband should be kept below 1 dB to ensure that low-frequency signals can pass effectively. Secondly, the filter's "roll-off slope" should be observed; a steeper slope indicates a clearer transition from the passband to the stopband, more effectively distinguishing between low-frequency and high-frequency signals. High-frequency suppression is also crucial; achieving -40 dB or -60 dB in the target stopband indicates excellent high-frequency filtering capability, effectively removing high-frequency noise and harmonics. Furthermore, the filter's stability under high power or temperature variations should be considered; excessive characteristic drift will affect the filtering effect. Combining the roll-off slope, suppression, and insertion loss (IL), the performance of an LPF can be determined.
3. Performance Evaluation of High-Pass Filters (HPF)
The key to evaluating the performance of a high-pass filter lies in its low-frequency blocking capability and high-frequency passband quality. First, it's crucial to ensure sufficient attenuation in the low-frequency region. Ideally, the target stopband should reach -30 dB to -50 dB to effectively isolate low-frequency noise, DC offset, or low-frequency interference. Second, the lower the insertion loss in the high-frequency passband, the better, indicating that high-frequency signals can pass through smoothly. Return loss in the passband is also an important indicator; a higher RL indicates better matching and less signal reflection. A steeper slope in the transition region indicates that the filter can more clearly separate low and high frequencies. Furthermore, high power tolerance and frequency stability are also important factors in evaluating the quality of an HPF. In summary, performance can be evaluated based on attenuation capability, passband IL, matching, and slope.
4. Performance Evaluation of Band-Stop Filters (BSF)
Evaluating the performance of a band-stop filter first requires checking its stopband depth and width. The core function of a notch filter is to suppress specific frequencies; therefore, a deeper stopband is better, typically -50 dB to -80 dB to ensure effective isolation of specific interference. The stopband width depends on the application requirements. A stopband that is too narrow may fail due to temperature drift, while a stopband that is too wide may inadvertently block other signals; therefore, a balance is necessary. Secondly, the passband insertion loss outside the stopband should be kept low to avoid affecting normal signals. Frequency stability is also crucial; if the stopband center drifts with temperature or power, the interference intended to be suppressed will be missed. Finally, the group delay of the filter should be observed to ensure it is not too large, as this could affect the integrity of the system's modulated signal. Performance can be evaluated by combining its stopband depth, passband IL, stability, and group delay.
Temwell Service in RF Filter
Temwell has been deeply involved in the RF and microwave filter field for nearly 30 years, possessing comprehensive design and development capabilities and stable mass production technology. We can assist customers in creating high-performance, customized filter solutions to meet their application needs. We are familiar with various RF architectures and frequency allocation requirements, and can provide professional parameter analysis, simulation design, sample fabrication, and measurement verification to meet the requirements of various communication and microwave systems.
Temwell services cover four main filter function types:
*BPF (Bandpass Filter): Allows signals to pass through a specific frequency band.
*LPF (Low-Pass Filter): Passes low frequencies and blocks high frequencies.
*HPF (High-Pass Filter): Passes high frequencies and blocks low frequencies.
*BSF (Band-Stop Filter): Suppresses specific interference frequencies.
Also supporting four major filter technology platforms:
*Helical Filter (High Q value, low loss)
*Cavity Filter (High power, high isolation)
*DR Filter (High stability, suitable for microwave bands)
*SAW Filter (Miniaturization, low cost)
Through the integration of multiple technology platforms, Temwell can provide filter solutions that best meet your performance, size, and cost requirements, making it your best RF technology partner.
If you are interested in Customized RF Filter Service, feel free to contact us and get free consultation services so that we can provide you with the best solution.
Subscribe to us on Facebook for the latest product news.
